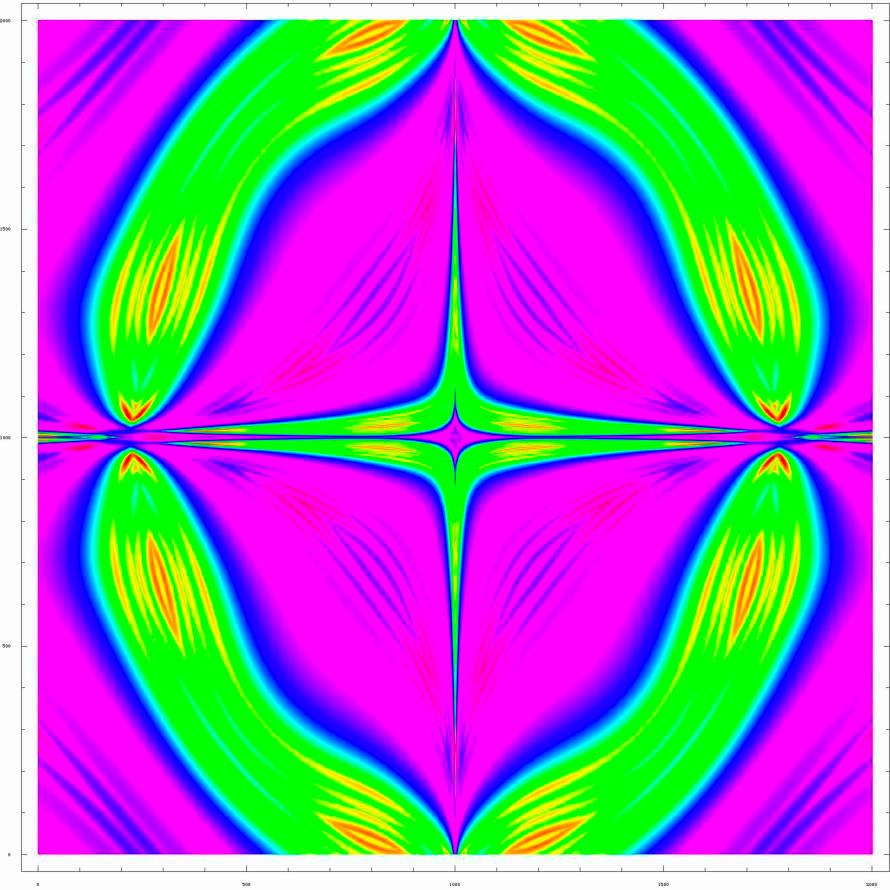
Mathematica Note Being on stage with Steve Jobs at a major product introduction keynote address is a thrill. I don't care how jaded you are, it's the kind of experience you should milk for all the excitement it's worth. For the Macintosh G5 introduction at WWDC in July 2003, I prepared this little fractal animation as a sort of graphical progress monitor showing off the speed with which the machine is able to do large integer multiplication operations. (Which has nothing to do with this particular fractal, by the way.) Of course, it also shows off some things Mathematica can do, which is ultimately why we agree to do these presentations for Apple in the first place. One of the points I made in my little segment was how the great speed of the G5 and the great power of Mathematica allowed me to play around with a huge number of possible fractals and parameter values until I found this really nice one. Sure, you could do something like that with a more primitive tools (i.e., any other tool), but could you do it in the half hour you can squeeze in between all the other things you're supposed to be doing? That's often the real test of what's possible, and Mathematica greatly expands the range of things you can do in a very short time. You can see a video of me on stage here, if Apple hasn't taken it down yet (they leave them up for about a year). Skip to 1:40:00 in to the video to find me. Or click the camera icon above to see a QuickTime animation showing how this fractal evolves as you change one of its parameters. Amazingly, all the incredibly variable features of this fractal are generated by the same same function, simply by varying a single parameter around an oval path in the complex plane. The fractal is nine iterations of the function: I (-Sqrt[Abs[im]] - Sqrt[Abs[re]] + 1)^2 + (0.6*(Cos[c] + 1) + 0.25*I*(Sin[c] + 1) + Sqrt[Abs[im]] - Sqrt[Abs[re]])^2 where re and im represent the real and imaginary parts of the value at a given point. The function is plotted from -1 to 1 and -I to I, and the animation consists of varying the parameter c from 0 to 2Pi.